196 Digital Data Acquisition
For whom intended: This course is intended for laboratory and field test technicians and engineers.
Course Description: The objective of the course is to provide participants with the knowledge required to specify, evaluate and use a wide variety of digital data acquisition systems in laboratory and field applications. Basic principles of sampling and digitizing theory are presented and reinforced with practical examples from everyday testing operations. Emphasis is placed on understanding the theoretical concepts through “mechanical feel” rather than mathematics.
 Hardware discussions concentrate on performance capabilities and practical problems that arise in laboratory and field applications.
Hardware discussions concentrate on performance capabilities and practical problems that arise in laboratory and field applications.
Heavy emphasis is placed on new technologies and system concepts that will be available in the near future. The aim is to prepare participants to design and procure state-of-the art systems that will satisfy their technical requirements efficiently and economically.
Literature describing the latest available hardware will be used as examples of good (and bad) practice. Special emphasis will be placed on critical evaluation of commercially-available hardware and software systems.
The course is presented as a series of highly interactive lecture/discussion sessions. Problems for individual and group solution are interspersed throughout the course to act as training aids and to evaluate class progress. Special-interest discussions are encouraged outside of the regular course sessions.
Diploma Programs This course is required for TTi’s Data Acquisition and Analysis Specialist (DAS) Diploma Programs. It may be used as an optional course for any other TTi specialist diploma program.
RELATED COURSES Course 194-3, Vibration and Shock Test Control Techniques, is combined with course 196 to form TTi open course 194.
Prerequisites: Participants should have attended TTi’s course, Instrumentation for Test and Measurement, or some equivalent training program. A good understanding of the engineering problem to be analyzed is expected. An understanding of basic computer and data acquisition principles will be useful.
Text Each student will receive 180 days access to the on-line electronic course workbook. Renewals and printed textbooks are available for an additional fee.
Internet Complete Course 196 features almost ten hours of video as well as more in-depth reading material. All chapters of course 196 are also available as OnDemand Internet Short Topics. See the course outline below for details.
Course Hourse, Certificate and CEUs Class hours/days for on-site courses can vary from 14–35 hours over 2–5 days as requested by our clients. Upon successful course completion, each participant receives a certificate of completion and one Continuing Education Unit (CEU) for every ten class hours.
Click for a printable course outline (pdf).
Course Outline
Chapter 1 - Course Overview, Objectives
- Objectives
- Theory
- Hardware
- Analysis
- System Specification and Evaluation
Chapter 2 - Role of Data Acquisition
- Experiment Mission
- Measurements/Transducers
- Specimen-to-Data-Acquisition Connection
- Data Acquisition
- Computer Interface
- “Computer”
- Data Storage
- Data Analysis
- Test/System Type Categorization
Chapter 3 - Basic Concepts and Terminology
- Time History
- Time-History Properties
- Spectra
- Time and Frequency Domain
- Spectrum Calculation ... Comb Filter Analogy
- The Spectral View
- The Fourier Transform .. Properties
- Time History/Spectra Examples
- Time History/Spectra Equivalence
- Transfer Functions
- Low Pass Filter—Transfer Function Interpretation
- Decibels
Chapter 4 - Accuracy, Precision, Errors and Dynamic Range
- Accuracy and Precision—Definition
- Measurement Model
- Ideal vs. Perfect
- The Transfer Function of Signal-Path Components
- The System Transfer Function
- Errors
- Deviations From the Assumed Model—Linearity
- Linearity Characterization
- Differential Nonlinearity
- Accuracy and Dynamic Range
- Dynamic Range
- Headroom—Designing for the Unexpected
- Finding Small Effects in Large Data
- Accuracy and Dynamic Range—How are they Quantified?
- Errors… Re: Full Scale or Re:Reading
- Errors.. Time-Domain Characterization… “DC” Accuracy
- SpecsManShip...Lying with Statistics
- A Diversion… What Does RMS Error Mean?
- Accuracy/Dynamic-Range Characterization
- Dynamic Range vs. Accuracy
- Sources of Error
- Bias and Random Errors
- Classical Error Analysis
- AC/DC Coupling
- “Out-of Band” Energy
Chapter 5 - Digitizing Theory
- Digitizing Theory—Bits, Bytes, Words
- Bytes
- Kilo, Mega, Giga, Terra, Peta…Googol
- Coding Conventions
- The Analog-to-Digital Transformation
- The BiPolar A-to-D...Offset Binary Coding
- A/D Conversion Characteristics
- A/D Conversion “Gross Errors”
- A/D Conversion “Small Errors”
- A/D Resolution
- Resolution vs. Number of Bits
- Full Scale Sine Input Dynamic Range—“Effective Bits Test”
- Dynamic Range—“Effective Bits Test” Spectral Calculation
- Real System Dynamic Range Characterization
- Dynamic Range…Zero-Input Response
- The Effect of Analysis Bandwidth
- How Many Bits are Needed?
- The “Effective Bits” Test
- “Effective Bits” Results
- What’s The Difference?
- Which Characterization Should be Used?
- An Alternate Effective Bits Calculation
Chapter 6 - Sampling Theory — Aliasing
- Sampling Theory—Digitizing “Rules”
- How Often to Sample?
- Conventional Wisdom
- Shannon’s Theorem
- Digitizing With various numbers of Points/Cycle
- Aliasing Example
- Aliasing: Correctly Sampled Set
- Aliasing: Undersampled Set
- Aliasing Example .. Comparison of Data Sets
- The Spectral View
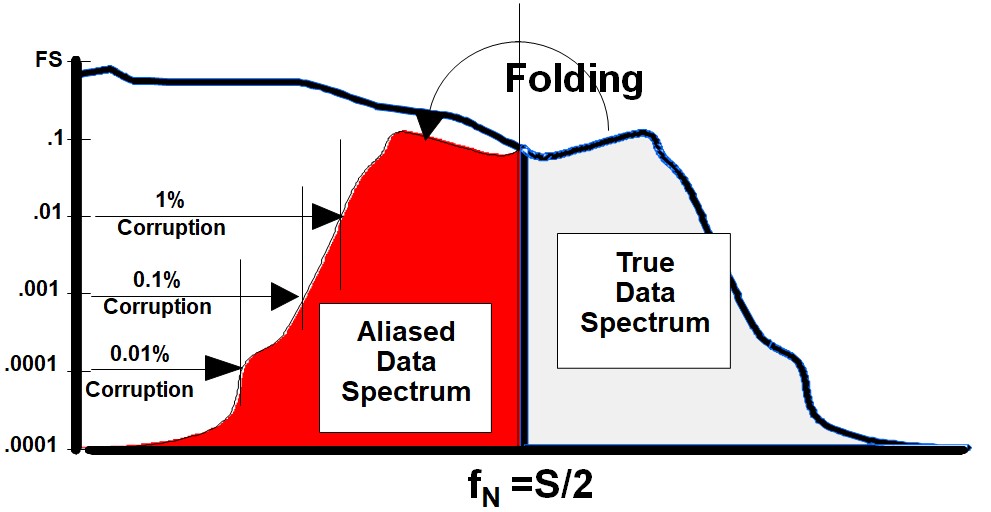
- Aliasing.. Viewed as Folding
- The Insidious Part
- Where Does the Aliased Data Appear?
- Aliasing Example .. Sine Signal
- Aliasing/Multiple Folding
- Another View of Folding (and a Trick!)
- The Way It has been Done So Far
- “Undersampling”
- The Aliasing Diagram
- Critical Points
Chapter 7 - Hardware
- System Elements
- Signal Conditioners
- Amplifiers
- Gain
- Common-Mode Rejection
- Measurements
- The Way it is Done
- The Ideal Differential Amplifier
- “Normal-Mode” Voltage
- Common Mode Voltage
- Common Mode Error
- Common Mode Rejection Ratio
- Problem .. Induced Noise
- Objective .. Reduce the Effects of Induced Noise
- Noise Rejection .. Differential Input
- Twisted Pair Conductors
- Shielding
- Shield Connection
- Shield Termination
- Balanced Input
- Amplifier Common
- Full Bridge
- Single-Arm Bridge
- Thermocouples
- The Real Differential Amplifier (and Source)
- Real Differential Amplifier and Source .. Effect
- Instrumentation Amplifier .. Implementation
- Power-Supply Restrictions
- Problem .. Measure Small Voltage Differences in a High Common-Mode Environment.
- Isolation Amplifier .. Concept
- IEPE Transducer Cabling
Chapter 8 - Alias Protection
- Pyrotechnic Test Data Set Example—Alias-Protection
- Solution #1: Sample Really Fast
- Solution #2: Analog Anti-Alias Filters
- Filters
- The Basic Low-Pass-Filter Concept
- Brick-Wall vs. Real Filters
- How Filters Behave
- Aliasing Analysis
- Anti-Alias Filters … Hardware
- Complex Filter “Construction”
- Building a Filter
- Group Delay
- “Classical” Filter Types
- Bessel Filters
- Butterworth Filters
- Elliptical Filters
- Low-Pass Filter Comparison… Spectral Domain
- Filter Characteristic
- Filter/Sample-Rate
- Trade-Offs
- Aliasing…Revisited
- Aliasing Analysis—Assumption #1—Physical Considerations
- Pyrotechnic Test Data Set
- Assumption #2…Filter Cutoff Frequency
- Aliasing Analysis—Assumption #1—Physical Considerations
- Sampling Ratio Calculation
- The fR /fCR Ratio
- Performance of Different Filters
- Minimum Sampling Ratios for Different Filters
- The Aliasing Diagram—Filter/Alias Analyzer
- Anti-Alias Filter Effect (1.61 Points/Cycle)
- Removing Aliased Data
- How to Tell Whether a Data Set is Aliased
- Good and Bad (Ugly)
- “Digital” Anti-Alias Filters
- AC/DC Coupling
- Why do AC Coupling?
- AC-Coupling to Remove Offset
- AC-Coupling Methods
- Capacitive AC Coupling
- Offset Subtraction … Analog
- Offset Subtraction … “Digital”
- Recommendation
- The Downside of AC-Coupling
- AC-Coupling Distortion—More Examples
Chapter 9 - Multiplexers
- Multiplexers—Function
- Types of Multiplexers
- Mechanical
- Solid State
- Single-Ended/Differential
- Multi-Tier
- Solid-State Multiplexers—Switching Time
- A Problem with Multiplexers—Crosstalk
- Sample and Hold Amplifiers
- Function
- Operation
- Real S&H Amplifiers
Chapter 10 - Analog-to-Digital Converters
- Analog-to-Digital Converters—Function
- Flash/Parallel A/D Converters
- Successive Approximation A/D Converters
- Digital-to Analog (D/A) Converter
- Successive Approximation Converters
- Operation
- Changing Signal
- Near ½ Scale
- Aliasing Protection
- Oversampling Converters
- Implementation
- Higher Speed
- The Solution… A 1-Bit Converter
- Sigma Delta (High-Ratio) Oversampling—Alias Protection
- Sigma Delta Modulation
- Sigma Delta Filter/Decimator
- Sigma-Delta A/D .. Actual Implementation
- Sigma-Delta Filter Characteristic
- Delay Characteristics
- Interesting Behavior
- System Applications
- Lower Sample Rates
- Sigma-Delta Converters Pro/Con
- Sampling Ratio Requirements (Revisited)
- The Alias Test—for Some SD Systems
- Sigma Delta—Caveat Emptor
- Averaging or Integrating A/D Converters
- Averaging A/D ..Principle
- Integrating Converters—Noise Rejection
- Dual-Slope A/D Converters
Chapter 11 - Real System Configurations
- The “Fundamental” Component(s)
- Minimum, Single-Channel System
- Single-Channel System with A-A Filter
- Multi-Channel .. A/D Per Channel
- Multi-Channel .. Minimum Multiplexed System
- Multi-Channel ..Differential Multiplexer
- Amplifier-Per-Channel Multiplexed System
- Amp/Filter-Per-Channel Multiplexed System
- Simultaneous Sample-and-Hold System
- Oversampling/Sigma Delta Converter System
- Transient Recorders/Digital Oscilloscopes
- Transient Recorder “Feature” .. Pre-Trigger
- “Transient Recorder” Extensions
Chapter 12 - The Computer and The Data Acquisition System
- Interfaces
- The Computer Interface
- Serial Interfaces (Classical)
- Serial Interfaces (Modern)
- Parallel Interfaces
- Data Transfer Concepts
- Data Transfer Mechanisms
- Programmed I/O
- DMA I/O
- Double-Buffering
- Chaining
- Getting Data to Storage
- Interrupts
- FIFO Memory
- “Hosts” and “Buses”
- The Computer
- Host Options for Data Acquisition
- PC-Computers .. Hardware.. 2013
- Getting Data to Disk
- Disk Fragmentation
- Disk Arrays
- RAID Disk Arrays
- JBOD Disk Array
- Transfers, Scans, and Buffers
- PC Systems (“Clones”)
- PC-Computers .. Software
- Buses
- The ISA Bus for Data Acquisition
- The PCI Bus for Data Acquisition
- The PCI-Express Bus for Data Acquisition
- The Compact PCI/PXI Bus
- The VME Bus
- The VXI Bus
- Universal Serial Bus (USB 2.0)
- Wi-Fi
- Ethernet (Gigabit)
- “Architectures”
- Performance Improvement vs. Time
- System Conception ... Questions
- PC System Architectures
- Peripheral Processors
- Eavesdropping
Chapter 13 - Data Analysis
- Counts to Engineering-Unit Conversion
- Counts-to-Volts Conversion
- Volts-to-Engineering Units (EU) Conversion
- Polynomial Approximation
- Linear Segment Approximation
- Noise Reduction, Smoothing and Filtering
- Noise Removal (Filtering)…“Smoothing by N”
- Noise Removal…Exponential Smoothing
- Exponential vs “by N” Smoothing…Time Response
- Exponential vs “by N” Smoothing…Filter Shape
- Filtering in the Spectral Domain
- Data Resampling (Interpolation)
- Time-Domain Interpolation
- Resampling/Interpolation…Example
- Pulse Interpolation Example
- Data Interpolation…When is it Needed?
- Instrumentation and Filter Distortion Correction
- DownSampling
- One Strategy (that Minimizes Sample Rate)
- Problem …. The System Transfer Function
- The Effect of Signal-Path Components
- Making Results Agree/What Does “Normalize” Mean?
- Defining a “Standard System Transfer Function”
- System Transfer-Function-Normalization Function
- Satisfying Standards (SAE)
- Recommendations
- Shock (SRS) Testing…
- Recommendation: Vibration & Acoustic Testing
- Removal of Aliased Data from Time Histories
- Time History Analysis-Alias Signal Rejection
- Sampling Strategy
- Analog (Anti-Alias Filter 4-Pole Bessel at 8 kHz)
- Analog Low-Passed—4 Pole Bessel at 8 kHz
- Acquired Data—20 K S/S
- Low Pass Filtered (Digital) at 4110 Hz
- A Better Sampling Strategy
Chapter 14 - System Specification and Evaluation
- The System-Specifier’s View
- Specification Topics
- System Accuracy Specification
- System Source Options
- The Vendor’s Job
- Evaluating Systems…Simple Tests
- Testing Toolkit
- Test 1: Shorted-Input Noise…the Simplest Test
- Test 2: Crosstalk
- Test 3: Frequency Response…In-Band Behavior
- Test 4: Frequency Response…Out-Of-Band Behavior
- Out-of-Band Behavior Analysis
- What Slew Rate is Required?
- Input Saturation Behavior
- Common-Mode Behavior (for Differential Systems)
- A More Critical Test…Effective Bits
- Effective Bits…the Basic Idea
- The Effective Bits Analyzer
- Analysis Steps
- Effective Bits---Error Calculations
- The Spectrum of the Error (Normalized)
- Some Effective Bits Results
- System Specs—What Do They Mean??
- Details on the “Standard” Test
- What Do Specific Users Care About?
Chapter 15 - Review and Summary
- Critical Points
- Dealing with the Pitfalls—Doing it Right
- Aliasing Errors
- Amplifiers and Cabling—Induced-Noise Rejection
- Anti-Alias Filter Distortion
- Predictions are Hard, Especially about the Future
- Test-Organization Philosophy
Appendix A - Glossary of Terms
Appendix B - Buzzwords and Jargon
Appendix C - Sample System Specification
Appendix D - Characterizing Errors and Dynamic Range SpecsManship...the Fine Art of Lying With Math & Statistics
Appendix E - Technical Articles and Demonstration Programs
Final Review
Award of Certificates for successful completion
Click for a printable course outline (pdf).
Revised 220512
